主成分分析(PCA)相关推导
我一直不知道特征值有什么用,直到我(
的膝盖中了一箭)学了PCA
主成分分析(Principal Component Analysis)是在数据降维和特征提取里常用的方法,又名Karhunen-Loève(K-L)变换。从光谱分解到eigenface,主成分分析有很广泛的应用,甚至如今大热的深度神经网络,某种程度上也有很多从PCA中得到的启发。根据之前blog中的一些数学方法,试着推导一下整个流程。在此之前,先来看看它的历史。。。。。。
History
- Karl Pearson于1901年提出
- Harold Hotelling于1933年加以发展
- Kari Karhunen和Michel Loève提出Karhunen-Loève threom
- Turk和Pentland于1991年正式提出eigenface的概念
关于PCA的推导大致有两种思路:
- 重建误差最小化
- 投影后方差最大化
其实这两种目标的最终优化函数是殊途同归的,下面开始进行推导
Proof
给定样本集
\[X= \lbrace \mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n \rbrace , \, \mathbf{x}_i \in R^d\],求投影矩阵$P_{m \times d} \, (1 \le m<d)$,使得通过投影 $\mathbf{y}_i=P(\mathbf{x}_i-\mu)$重构出的样本$\mathbf{\hat x}_i=P^T\mathbf{y}_i$的误差最小,即最小化
\[e=\sum_{i=1}^n \Vert (\mathbf{x_i}-\mu)-\mathbf{\hat x}_i \Vert^2\]。此处先用重建误差最小来推导,后面会看到具体的形式上的一致。这里样本减去均值$\mu=\frac1n\sum_{i=1}^n \mathbf{x}_i$再投影,目的是将样本空间的原点移动到均值点,然后再投影,如下图
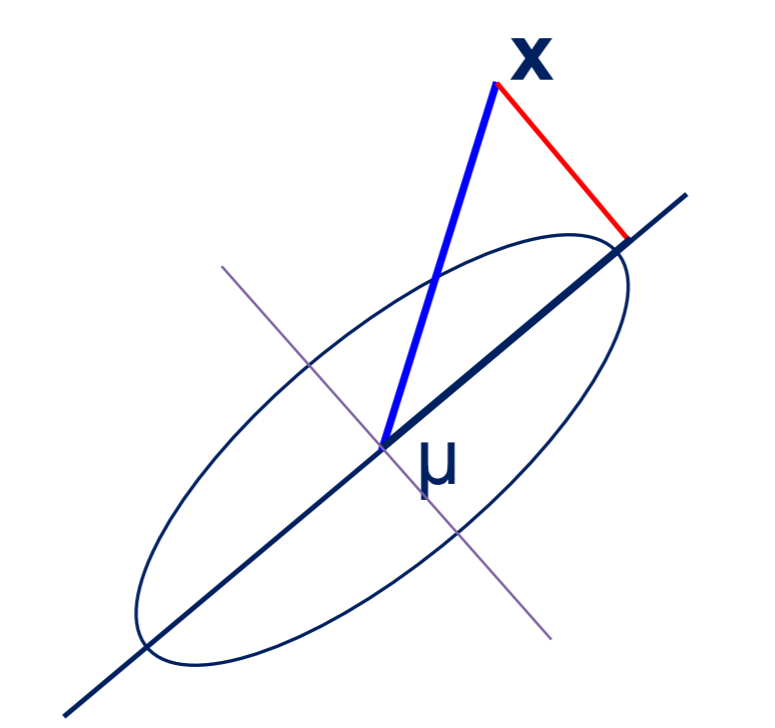
考虑最极端的情况,当$m=1$时,即将原样本空间投影到1维,此时矩阵$P$退化为行向量$\mathbf{p}_1$,$\mathbf{p}_1$即为第一主成分。接下来计算一下第一主成分,为了更好地表达该问题,我们将它写成一个约束极值问题如下:
\[\min_P \sum_{i=1}^n \Vert (\mathbf{x_i}-\mu)-\mathbf{\hat x}_i \Vert^2\\ s.t. \quad \mathbf{p}_1\mathbf{p}_1^T=1\]上面给出的约束是$\mathbf{p}_1\mathbf{p}_1^T=1$,归一化操作会有更好的性质。这里从另一个角度解释一下,对于重建的样本$\mathbf{\hat x}_i$我们希望再投影回去时,与原来的投影$\mathbf{y}_i$相等,即有$\mathbf{y}_i=\mathbf{p}_1\mathbf{\hat x}_i=\mathbf{p}_1\mathbf{p}_1^T\mathbf{y}_i$。
接下来就是运用拉格朗日乘数法来对该约束极值问题进行求解。因为目标函数是一个标量,所以可以将它套上一个迹函数即
\[\mathrm{tr}(\sum_{i=1}^n \Vert (\mathbf{x_i}-\mu)-\mathbf{\hat x}_i \Vert^2)\\ \Downarrow \\ \sum_{i=1}^n \mathrm{tr}(\Vert (\mathbf{x_i}-\mu)-\mathbf{\hat x}_i \Vert^2)\\ \Downarrow \\ \sum_{i=1}^n\mathrm{tr}\{[(\mathbf{x}_i-\mu)-\mathbf{\hat x}_i]^T[(\mathbf{x}_i-\mu)-\mathbf{\hat x}_i]\}\]将内部的重构样本展开得到
\[\sum_{i=1}^n\mathrm{tr}\{[(\mathbf{x}_i-\mu)-\mathbf{p}_1^T\mathbf{p}_1(\mathbf{x}_i-\mu)]^T[(\mathbf{x}_i-\mu)-\mathbf{p}_1^T\mathbf{p}_1(\mathbf{x}_i-\mu)]\}\\ \Downarrow\\ \sum_{i=1}^n\mathrm{tr}[(\mathbf{x}_i-\mu)^T(\mathbf{x}_i-\mu)-2(\mathbf{x}_i-\mu)^T\mathbf{p}_1^T\mathbf{p}_1(\mathbf{x}_i-\mu)+(\mathbf{x}_i-\mu)^T\mathbf{p}_1^T\mathbf{p}_1(\mathbf{x}_i-\mu)]\]舍去与参数$P$的无关项,可以得到
\[\sum_{i=1}^n\mathrm{tr}[-(\mathbf{x}_i-\mu)^T\mathbf{p}_1^T\mathbf{p}_1(\mathbf{x}_i-\mu)]\]最小化该目标函数等价于最大化
\[\sum_{i=1}^n\mathrm{tr}[(\mathbf{x}_i-\mu)^T\mathbf{p}_1^T\mathbf{p}_1(\mathbf{x}_i-\mu)]\]再加上拉格朗日乘数项得到最终的无约束目标函数
\[\sum_{i=1}^n\mathrm{tr}[(\mathbf{x}_i-\mu)^T\mathbf{p}_1^T\mathbf{p}_1(\mathbf{x}_i-\mu)]-\lambda(\mathbf{p}_1\mathbf{p}_1^T-1)\]利用迹的性质,再化简一下
\[\sum_{i=1}^n\mathrm{tr}[(\mathbf{x}_i-\mu)(\mathbf{x}_i-\mu)^T\mathbf{p}_1^T\mathbf{p}_1]-\lambda(\mathbf{p}_1\mathbf{p}_1^T-1)\]令$S=\sum_{i=1}^n(\mathbf{x}_i-\mu)(\mathbf{x}_i-\mu)^T$,$S$即为离散度矩阵 ,代入目标函数得到
\[\mathrm{tr}(\mathbf{p}_1S\mathbf{p}_1^T)-\lambda(\mathbf{p}_1\mathbf{p}_1^T-1)\]对比一下投影后的方差最大的目标函数,假设令$S=\frac1n\sum_{i=1}^n(\mathbf{x}_i-\mu)(\mathbf{x}_i-\mu)^T$,$S$即为协方差矩阵,
\[\mathrm{tr}(\mathbf{p}_1S\mathbf{p}_1^T)-\lambda(\mathbf{p}_1\mathbf{p}_1^T-1)\]可以看到实际的优化目标是一致的,这里$S$中的$\frac1n$与最大化参数$\mathbf{p}_1$无关,结果上可以等价。
求目标函数对$\mathbf{p}_1$的导数并令其为0可得
\[\mathbf{p}_1S=\lambda \mathbf{p}_1\]因为$\mathbf{p}_1$为行向量,$S$是实对称的,将整个式子转置一下
\[S\mathbf{p}_1^T=\lambda\mathbf{p}_1^T\]即$\mathbf{p}_1^T$为$S$的特征向量。那么原来的目标函数有
\[\mathbf{p}_1S\mathbf{p}_1^T=\lambda\mathbf{p}_1\mathbf{p}_1^T=\lambda\]所以当$\mathbf{p}_1^T$为$S$的最大特征值对应的特征向量时,目标函数达到最大值。
接下再看第二主成分,我们希望$\mathbf{p}_1^T,\mathbf{p}_2^T$构成一个正交的投影空间,同时希望除$\mathbf{p}_1^T$外,$\mathbf{p}_2S\mathbf{p}_2^T$最大。回想之前“特征值、特征向量和相似矩阵”中实对称矩阵的性质,刚好$S$的特征向量之间互相正交,所以很自然地将第二大特征值对应的特征向量与$\mathbf{p}_2^T$对应。后面的第三、四主成分自然与之类似。
再回过头来看,矩阵$S$的所有特征向量组成了一个旋转矩阵,在以均值点为原点的空间上对原样本空间进行旋转。而数据的离散程度用欧式距离在度量,线性空间中的正交变换并不影响欧式距离。后面的特征值部分可以与Rayleigh熵对比来看,Courant-Fischer定理等等。
Others
对于PCA的改进和应用列举一些:Kernel PCA, Robust PCA, PCA-SIFT, Eigenface, 3DMM
对比autoencoder的编码和解码,是不是很类似于PCA中的投影和重建呢?
Reference
UCAS-AI模式识别2018-16-特征提取与选择01
UCAS-AI计算机视觉cv-11
UCAS-AI计算机图形学-人脸动画
可以与TSNE降维方法一起对照,二者一起比较着学习。
| 微信(WeChat Pay) | 支付宝(AliPay) |

|

|
| 比特币(Bitcoin) | 以太坊(Ethereum) |

|

|
| 以太坊(Base) | 索拉纳(Solana) |

|

|