Simple Polygonal Mesh Structure
Euler’s Formula: V-E+F=2
A mesh is a manifold if each edge closed fan is incident to only one or two faces and the faces incident to a vertex form a closed or an open fan.

Manifold Conditions:
- Each edge is incident to only one or two faces.
- The faces incident to a vertex form a closed or an open fan.
A triangle mesh can be a manifold with boundary only if the following two local conditions are satisfied:
- Every edge is shared by one or two triangles
- Every vertex connects to a single edge-connected set of triangles
By convention, triangles of a manifold are oriented so that from the outside, the triangle is counter-clockwise (and seen from the inside it is clockwise).
Not all manifolds are orientable. The most wellknown ones are Möbius band and Klein bottle.


Since meshes are usually large and complex and since many operations are performed on meshes, complicated data structures that support efficient algorithms are needed.
Depending on the applications in hand, one may use vertex(or point)-based, edge-based, face-based, or other data structures.
Separate triangles mesh
Each triangle is an object that stores the coordinates of its vertices. This is a kind of face-based data structure. The simplest way to represent a surface mesh consists of storing a set of individual polygonal faces represented by their vertex positions (the socalled face-set).
struct SepTriangle{
double point1[3];
double point2[3];
double point3[3];
}; //simply stores the 3 vertices' coordinates
However, without additional connectivity information, this data structure requires expensive searches to recover the local adjacency information of a vertex and hence is not efficient enough for most algorithms.
Shared vertex mesh
Each vertex is an object that stores its three coordinates, each triangle is an object that stores reference to its vertices.
#define MAX_NUM_OF_VERTICES 10000
struct Vertex{
double x,y,z;
};
struct Vertex points[MAX_NUM_OF_VERTICES];
struct Triangle{
unsigned int index_v1,index_v2,index_v3;
};
Indexed triangle mesh
Same as shared vertex mesh but the j-th vertex of the i-th triangle is addressed as $Array[i][j], j=1,2,3$ and $i=1,2,\cdots,No.$ of triangles.
#define MAX_NUM_OF_VERTICES 10000
#define MAX_NUM_OF_TRIANGLES 6000
struct Vertex{
double x,y,z;
};
struct Vertex points[MAX_NUM_OF_VERTICES];
unsigned int triangles[MAX_NUM_OF_TRIANGLES][3];
Winged-edge
Stores connectivity at edges instead of vertices. Assign a direction to an edge, then it has two neighbor triangles. According to that, we can find the next edge in the left triangle and the right. So do the previous edges.
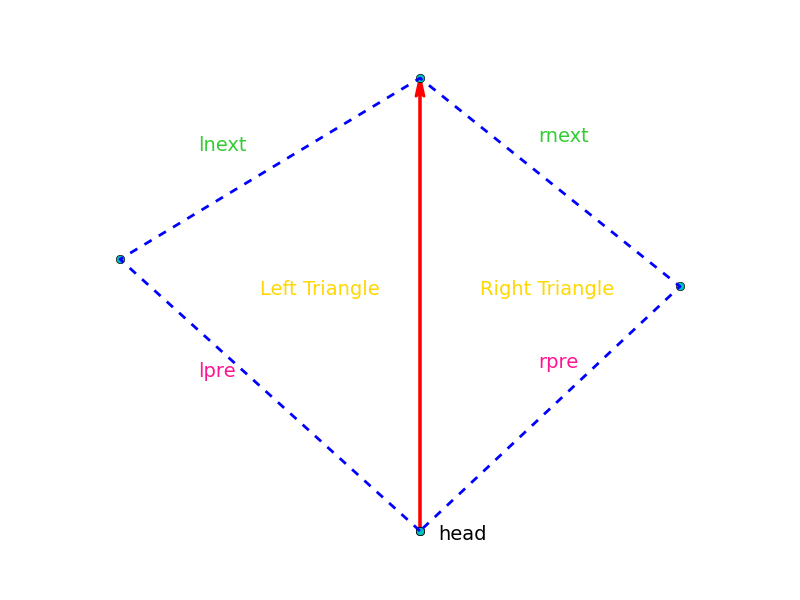
struct WingedEdge{
WingedEdge lpre, rpre, lnext, rnext;
Vertex head;
Triangle left, right;
};
struct Vertex{
double x,y,z;
};
Half-edge
However, the arbitrary orientation of edges makes traversal of the boundary of a face awkward while using the winged-edge structure. Every edge is split into 2 half-edge. In the half-edge structure, every half-edge is incident only to the face to its left(by convention).
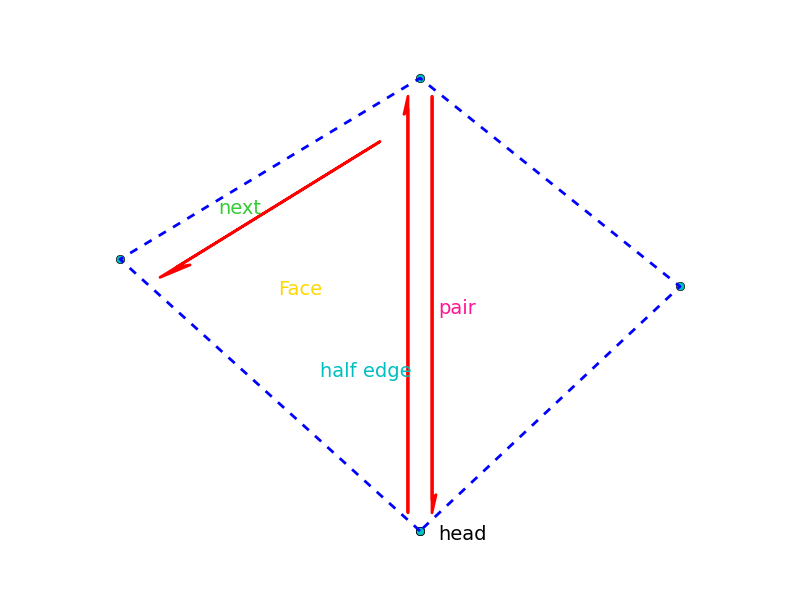
struct HalfEdge{
HalfEdge next,pair;
Vertex head;
Face f;
};
struct Vertex{
double x,y,z;
};
struct Face{
HalfEdge h;// any incident half-edge in its boundary
};
| 微信(WeChat Pay) | 支付宝(AliPay) |

|

|
| 比特币(Bitcoin) | 以太坊(Ethereum) |

|

|
| 以太坊(Base) | 索拉纳(Solana) |

|

|