数学杂记--调和级数的相关证明
1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+…
调和级数是所有正整数倒数之和: $\sum\limits_{n=1}^{\infty}\frac1n$,该级数是发散的。对于这一点可以从简单的积分得到证明:$\int_1^x\frac{1}{t}\mathrm{d}t=\ln x$,那么有
\[\int_n^{n+1}\frac1x\mathrm{d}x=\ln (1+\frac1n)\]根据拉格朗日中值定理,存在$n<\xi<n+1$,使得:
\[\int_n^{n+1}\frac1x\mathrm{d}x=\ln(1+\frac1n)=\frac1\xi<\frac1n \tag{1.1}\label{1.1}\]所以有
\[\sum_{n=1}^\infty\frac1n>\sum_{n=1}^{\infty}\ln(1+\frac1n)=\lim_{n\to\infty}\ln n\]故调和级数发散。参考下图:
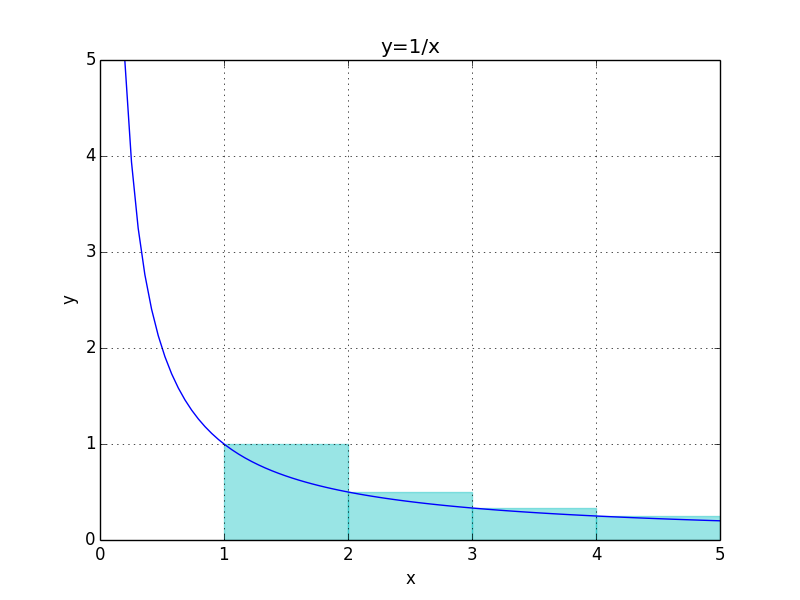
青色部分面积即为调和级数,函数曲线与$x$轴和$x=1,x=n$围成的面积就是$\ln n$,从图中可以看到青色部分面积更大。而根据$\eqref{1.1}$可以得到另一个结论:
\[\frac1{n+1}<\ln(1+\frac1n)\]两边再求和我们可以得到:
\[\sum_{n=1}^{\infty}\frac1{n+1}<\ln n<\sum_{n=1}^{\infty}\frac1n\]如下图:
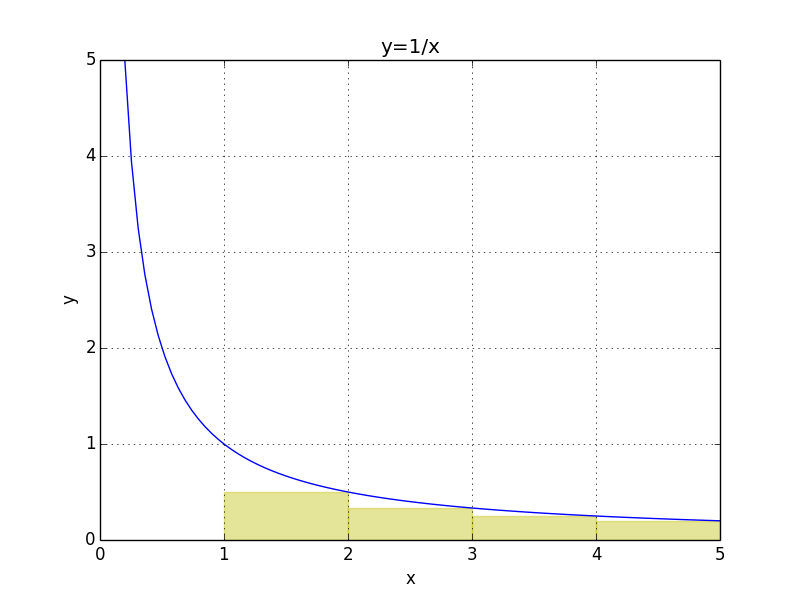
即$\ln n$与$n$的调和级数误差在1以内。 接下来看看函数$y=\frac1x$在$x\in(0,1)$的部分,反常积分$\int_0^1\frac1x\mathrm{d}x$发散。将它转换成黎曼和的形式,首先将区间$(0,1)$分割成$m$个部分,对于第$n$个柱形,其高为$y=\frac mn$,宽为$\frac1m$,所以面积之和为:
\[\frac1m \sum_{n=1}^{m} \frac mn = \sum_{n=1}^{m}\frac1n\]如下图是$m=5$时的分割:
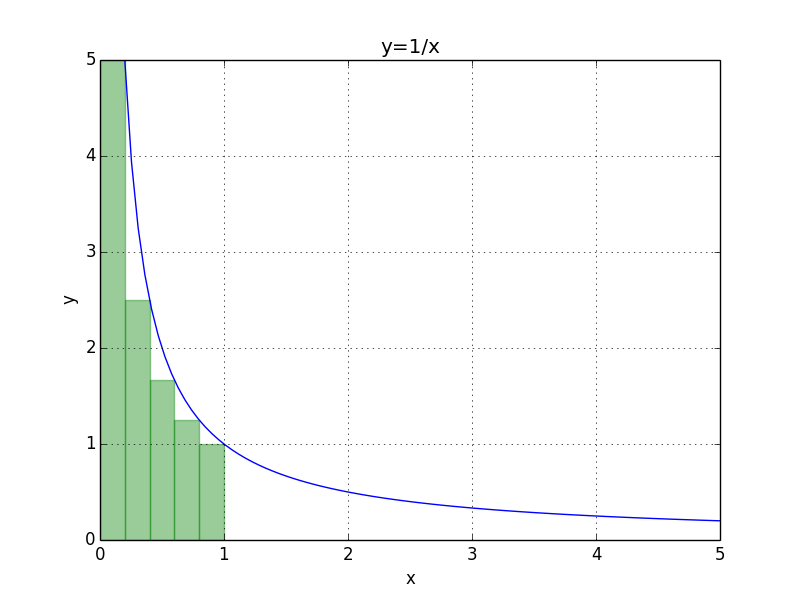
若对$m$取极限,那么有
\[\lim_{m \to \infty}\sum_{n=1}^{m}\frac1n=\sum_{n=1}^\infty\frac1n=\int_0^1\frac1x\mathrm{d}x\]依然可以看到调和级数是发散的,而且$n$越大,调和级数与$\ln n$越接近。回到$\eqref{1.1}$,我们可以从中得到另外一个重要的极限。对不等式两边都乘以$n$ 可以得到:
\[\frac n{n+1}<n\ln(1+\frac1n)<1\] \[\Downarrow\] \[\mathrm{e}^{1-\frac1{n+1}}<(1+\frac1n)^n<\mathrm{e}\]用夹逼定理取极限,就可以得到一个重要的极限:
\[\lim_{n\to\infty}(1+\frac1n)^n=\mathrm{e}\]与调和级数相反,$\sum\limits_{n=1}^{\infty}\frac1{n^2}$确是收敛的,可以很容易地通过比较判别法来证明:
\[\sum_{n=1}^{\infty}\frac1{n^2}<1+\sum_{n=2}^{\infty}\frac1{n(n-1)}=\lim_{n\to\infty}2-\frac1n=2\]具体到求取该级数,可以通过下面的方法: 考虑将函数$f(x)=2+\left| x \right|,-1\le x \le 1$展开成以2为周期的傅立叶级数。由于$f(x)$为偶函数,直接展开为余弦级数。
\[a_n=2\int_0^1(2+x)\cos(n\pi x)\mathrm{d}x=\frac2{n^2\pi^2}\left[(-1)^n-1 \right],n=1,2,...\] \[a_0=2\int_0^1(2+x)\mathrm{d}x=5\]观察$a_n$可知,$a_{2k}=0$。所以$f(x)$的傅立叶展开为:
\[f(x)=\frac52-\frac4{\pi^2}\sum_{k=0}^{\infty}\frac{\cos(2k+1)\pi x}{(2k+1)^2},x\in[-1,1]\]令$x=0$可得:
\[2=\frac52-\frac4{\pi^2}\sum_{k=0}^{\infty}\frac{1}{(2k+1)^2}\] \[\Downarrow\] \[\sum_{k=0}^{\infty}\frac{1}{(2k+1)^2}=\frac{\pi^2}8\]再来看看原来的级数,
\[\sum_{n=1}^{\infty}\frac1{n^2}=\sum_{k=0}^{\infty}\frac{1}{(2k+1)^2}+\sum_{k=1}^{\infty}\frac{1}{(2k)^2}=\sum_{k=0}^{\infty}\frac{1}{(2k+1)^2}+\frac14\sum_{n=1}^{\infty}\frac{1}{n^2}\] \[\Downarrow\] \[\sum_{n=1}^{\infty}\frac1{n^2}=\frac43\sum_{k=0}^{\infty}\frac{1}{(2k+1)^2}=\frac{\pi^2}6\]在$\frac1{n^2}$和$\frac1n$之间的级数还有发散的,比如$\sum\limits_{n=1}^\infty\frac1{n\ln n}$,很容易通过比较判别法去证明
\[\frac1{n\ln n}>\int_n^{n+1}\frac1{x\ln x}\mathrm{d}x\]| 微信(WeChat Pay) | 支付宝(AliPay) |

|

|
| 比特币(Bitcoin) | 以太坊(Ethereum) |

|

|
| 以太坊(Base) | 索拉纳(Solana) |

|

|